最も美しいとされる比率「黄金比」
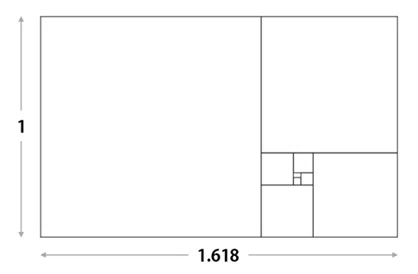
「黄金比」とは、近似値1:1.618、約5:8の安定的で最も美しい比率とされる貴金属比の一つです。1:(1+√5)÷2
黄金比を発見したのは、エウドクソス(紀元前408年頃から紀元前355年頃)で、その後、古代日リシアの彫刻家であるペイディアスが初めてパルテノン神殿建設時に使ったと言われています。

エウドクソス
紀元前4世紀の古代ギリシアのクニドス出身の数学者・天文学者。エジプトで長く暮らし、後にアテネに移住した。著作は現存せず、その仕事は後世の他の学者の引用によって現在に知られる。Wikipedia引用
1:(1+√5)/2 ≒ 1:1.618 は、人間が本能的に美しいと感じる比率だとされています。
「黄金比」という名前を付けたのはイタリアのレオナルド・ダ・ヴィンチであるという説もありますが、1835年刊行のドイツの数学者マルティン・オームの著書「初等純粋数学」に、「黄金比」という言葉が既に登場しています。 mathemathe「歴史上の数学者たち」から引用
1800年代に入ると人類が最も美しいと感じる比率と広く知れ渡り、「黄金比」と呼ばれるようになります。
海外の建築物では、サグラダ・ファミリア、日本でも鹿苑寺金閣をはじめとした建築物に用いられ、時代や国境を越えて人々を魅了している比率です。

この黄金比は自然界にも多く存在しており、松ぼっくりのかさ、花びら、葉の生え方においても黄金比を発見することができます。
黄金比を使った代表的な例として、ピラミッド、ミケランジェロのシスティーナ礼拝堂にある天井画のアダムの創造、ミロのヴィーナス、パルテノン神殿、名刺、はがき、Appleのロゴなどがあります。

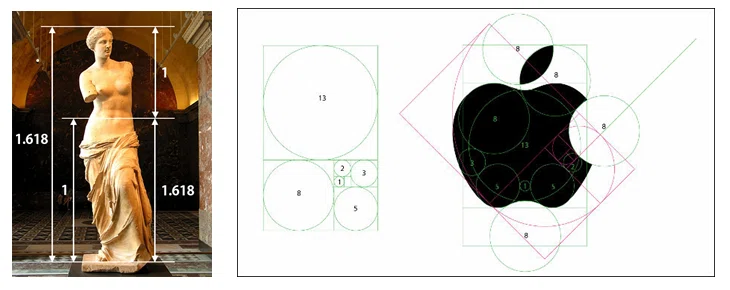
レオナルド・ダ・ヴィンチが描いた有名な絵画、「モナリザの微笑」も黄金比が使われている代表的なもののひとつです。モナリザの顔を細かく見ていくと、生え際から顎先までが綺麗に黄金比で成り立っています。

黄金比の長方形から、最大の正方形を除き、同様のことを続けると正方形が集まった形になっています。
参考資料/https://ferret-plus.com/1494
画像引用/https://www.asobou.co.jp/blog/web/golden-rate https://www.gizmodo.jp/
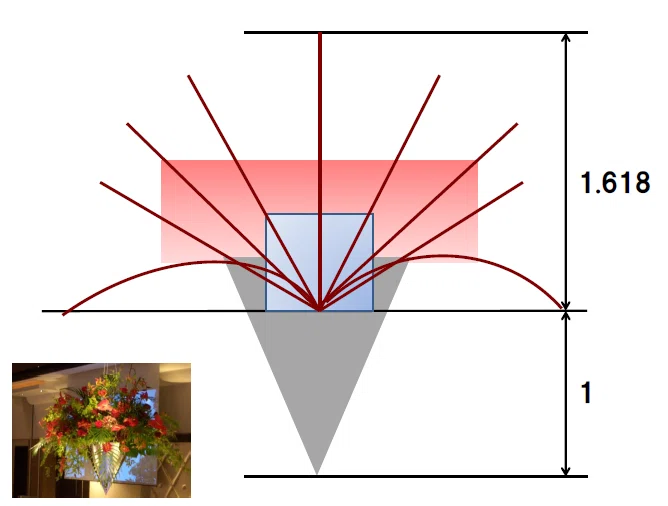
5階クラブ・モーガンで人気のコーディネート“吊り花”は、黄金比を意識してフラワーアレンジを行っています。
株式会社マグリット
専務取締役 羽原正人
THE MAGRITTE @partylabo.







